随着科技的发展,计算机在各个领域的应用越来越广泛。其中,电脑函数最大值最小值公式在数学建模和优化问题中具有重要作用。本文将深入探讨这一主题,介绍电脑函数最大值最小值公式的应用及其优势。

1.构建数学模型:将实际问题转化为数学模型是解决问题的关键。电脑函数最大值最小值公式能够帮助我们构建准确的数学模型,从而更好地理解问题的本质。
2.寻找函数的最大值与最小值:通过使用电脑函数最大值最小值公式,我们可以轻松地找到函数的最大值和最小值。这为解决许多实际问题提供了方便和效率。

3.优化问题的求解:很多实际问题都可以归结为优化问题,即在一定条件下求解使目标函数取得最大或最小值的变量取值。电脑函数最大值最小值公式为我们提供了一种优化算法,能够快速求解这类问题。
4.非线性函数的分析:很多实际问题中的函数往往是非线性的,传统的解析方法难以得到准确解。而电脑函数最大值最小值公式通过数值计算的方式,能够更好地分析非线性函数的特性。
5.约束条件的考虑:在实际问题中,往往存在一些约束条件。电脑函数最大值最小值公式能够将约束条件纳入考虑,并在满足约束条件的前提下找到最优解。
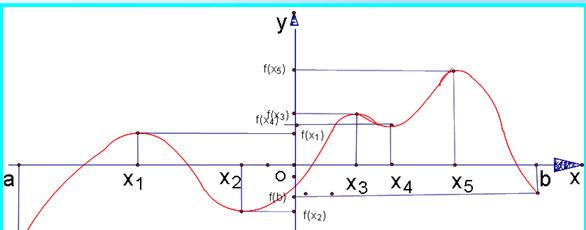
6.经济学领域的应用:电脑函数最大值最小值公式在经济学领域有广泛的应用。例如,在确定市场需求曲线和供给曲线交点时,可以使用该公式求解。
7.工程优化问题:工程中的许多问题需要进行优化设计,例如建筑结构、输电线路等。电脑函数最大值最小值公式可以帮助工程师找到最佳设计方案。
8.生产计划的优化:在生产管理中,合理安排生产计划可以降低成本、提高效率。电脑函数最大值最小值公式可以帮助我们优化生产计划,实现生产效益的最大化。
9.金融领域的应用:在金融风险管理中,电脑函数最大值最小值公式能够帮助分析人们的投资组合,并找到最佳的风险-收益平衡点。
10.运输与物流优化:电脑函数最大值最小值公式在运输与物流领域的应用非常广泛。例如,帮助确定最佳配送路线和货物装载方式等。
11.环境保护问题的解决:电脑函数最大值最小值公式在环境保护领域有着重要的应用。例如,在研究气候变化和减少污染排放时,可以使用该公式对相关数据进行优化分析。
12.能源规划与调度:对于能源供应和调度问题,电脑函数最大值最小值公式可以提供有效的计算工具,帮助能源规划者制定合理的决策方案。
13.决策支持系统:电脑函数最大值最小值公式为决策支持系统提供了重要的计算手段,帮助决策者做出最优决策。
14.教育教学中的应用:在教学中,通过电脑函数最大值最小值公式的应用,可以帮助学生更好地理解和应用数学知识。
15.研究领域的发展:电脑函数最大值最小值公式的应用为各个研究领域提供了新的思路和工具,推动了科学研究的进步。
通过对电脑函数最大值最小值公式的应用与优势的探讨,我们可以看到它在解决实际问题中的重要性和价值。无论是在工程、经济、环境还是教育等领域,该公式都能够发挥其独特的作用,为问题解决提供了便利和效率。深入研究和应用电脑函数最大值最小值公式将有助于推动各个领域的发展。